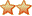Wzór na ciąg

Darlington · Postautor: **Darlington** » 31 mar 2009, o 20:41

Witam, przy obliczaniu szeregu Fouriera natrafiłem na parametr (cos(k•Π/2))/k•Π czyli na cykliczny ciąg o powtarzającej się liczbie 4 elementów:
0, -1, 0, 1, ...
czyli 0, -1, 0, 1, 0, -1, 0, 1, 0, -1, 0, 1, 0, -1, 0, 1, 0, -1, 0, 1, 0, -1, 0, 1,

I szukam wzoru mogącego opisac ten ciąg...

piotr_go · Postautor: **piotr_go** » 1 kwie 2009, o 10:24

cos (90*x) ?

Darlington · Postautor: **Darlington** » 1 kwie 2009, o 13:44

Hmm to by się zgadzało ale szukałem wzoru bez użycia funkcji trygonometrycznych, np (-1)^k

tg3a · Postautor: **tg3a** » 1 kwie 2009, o 18:22

A czy może być być funkcja int(x), która odrzuca część ułamkową argumentu, oraz funkcja mod (modulo), zapisywana w językach programowania znakiem % (określająca resztę z dzielenia pierwszego argumentu przez drugi)?
Jeśli tak, to może w ten sposób:
int((3-(k%4))/3)-int((k%4)/3)
lub, jak kto woli,
int(((k+2)%4)/3)-int((k%4)/3)
Niestety, nic prostszego nie potrafiłem wymyślić. Funkcja int w przypadku języka programowania używającego różnych typów zmiennych (a jedyny, jaki znam, który tego nie ma, to Spectrum Basic) jest niepotrzebna - w przypadku dzielenia dwóch liczb typu całkowitego część ułamkowa jest odrzucana automatycznie.
W sensie matematycznym uważam, że funkcje trygonometryczne są bardziej "eleganckie", ale gdyby chodziło o liczenie na komputerze, to lepsze jest użycie dzielenia całkowitego i funkcji/operatora modulo (%).
Pozdrawiam.
P.S. Jeszcze wspomnę o bardzo eleganckim matematycznie rozwiązaniu, które wymaga użycia rachunku liczb zespolonych:
(j^k +(-j)^k)/2
gdzie j oznacza jednostkę urojoną, czyli √(-1)

piotr_go · Postautor: **piotr_go** » 2 kwie 2009, o 10:39

Czy to ma być w jakimś programie?
Jeśli tak to prościej zrobić tablice z tymi 4rema elementami a jej adres dać AND 3.

Darlington · Postautor: **Darlington** » 2 kwie 2009, o 16:40

Już nie ważne ale dzięki za pomoc.

Wzór na ciąg

Kto jest online