Na razie wykonałem graf i chciałbym się dowiedzieć czy jest on poprawnie narysowany, bo jeśli jest źle to dalsze działania nie mają sensu.
Tzn.
Rozwiązanie zadania ma zawierać następujące elementy.
1. Graf stanów projektowanego układu (automatu) asynchronicznego.
2. Pierwotną tablicę przejść-wyjść układu.
3. Minimalizację liczby stanów wewnętrznych automatu.
4. Minimalne TPW automatu Moore'a oraz Mealy'ego. W tablicy wyjść automatu Mealy'ego należy wpisać wartości 0 lub 1 tylko w kratki odpowiadające stanom stabilnym w tablicy przejść. Pozostałe kratki tablicy wyjść należy wypełnić stanami nieokreślonymi.
5. Kodowanie stanów wewnętrznych automatu oraz zakodowane TPW More'a i Mealy'ego. Tablice należy zakodować wykorzystując jak najmniejszą liczbę zmiennych wewnętrznych. Zakodowane TPW nie mogą zawierać wyścigów krytycznych.
6. Minimalne formuły boolowskie dla funkcji wzbudzeń przerzutników oraz funkcji wyjść układu. Do realizacji układu można wykorzystywać asynchroniczne przerzutniki następujących typów :
- przerzutnik sr
- przerzutnik t
7. Schemat serwisowy (tj. schemat narysowany zgodnie z normą Mil. Std. 803b) oraz montażowy projektowanego układu. Rysując schemat można wykorzystywać wyłącznie symbole następujących elementów:
- bramka NOT (bramka negacji),
- 2-, 3- i 4-wejściowa bramka NAND,
- 2-, 3- i 4-wejściowa bramka NOR,
- 2-wejściowa bramka XOR.
- asynchroniczny przerzutnik t
Dodam jeszcze że zawory i grzałka załączane są stanem niskim ("0"):
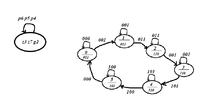
Z góry dziękuje za pomoc.
Pozdrawiam